Leetcode题解剑指 Offer 07. 重建二叉树

PROBLEM

难度中等

MY ANSWER

递归

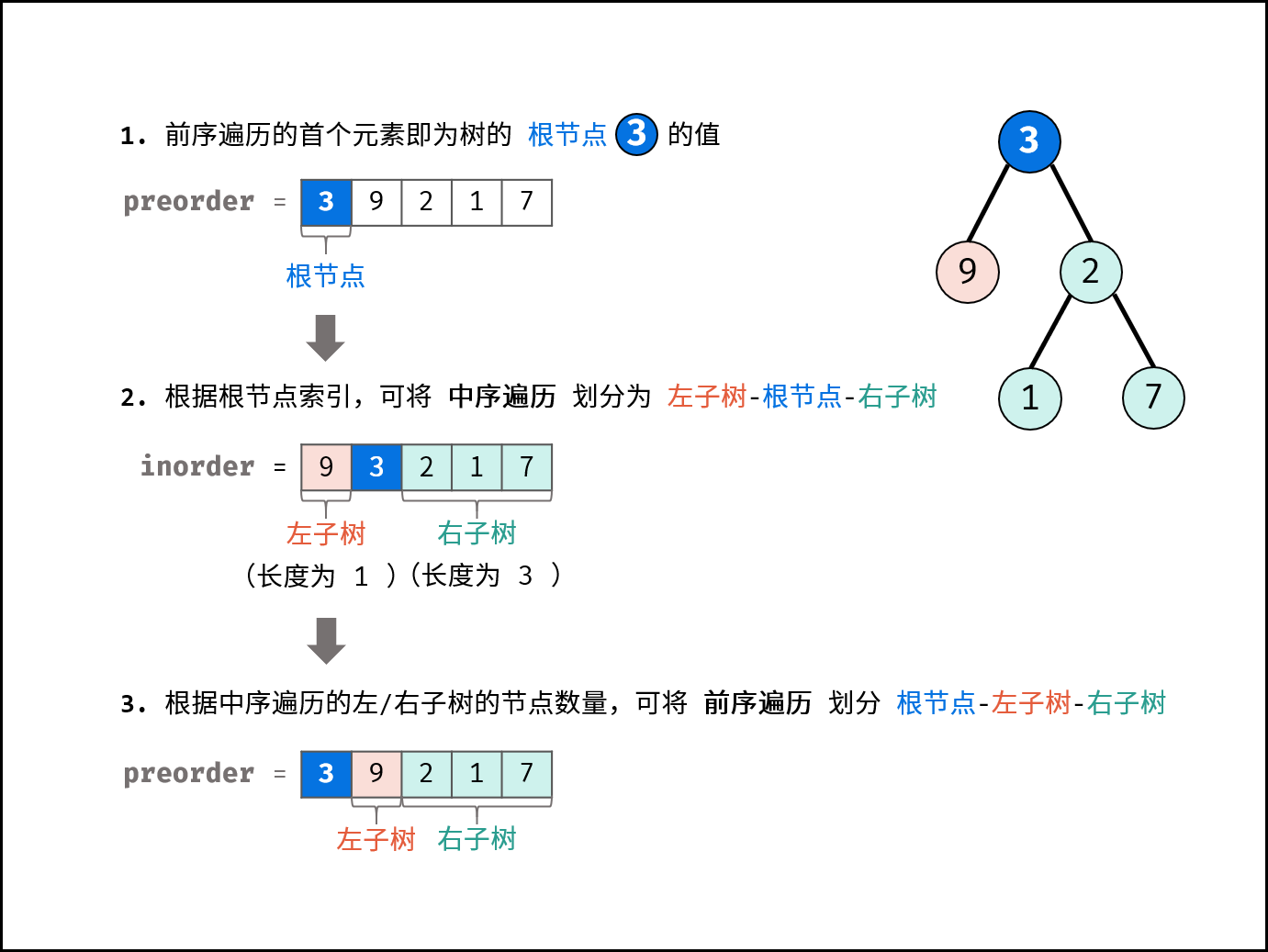
思路如图，顺着设计递归解决。使用哈希表来查询root在inorder中的索引减少时间复杂度。递归函数settree中，参数root为根节点在preorder中的索引，参数left为inorder中根节点的子树的左边界，参数right为inorder中根节点的子树的右边界。时间复杂度O(n)，空间复杂度O(n)。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> index;
    vector<int> preorder;
    TreeNode* settree(int root, int left, int right) {
        if(left > right) {
            return nullptr;
        }
        TreeNode* t = new TreeNode(preorder[root]);
        t->left = settree(root + 1, left, index[preorder[root]] - 1);
        t->right = settree(root + index[preorder[root]] - left + 1, index[preorder[root]] + 1, right);
        return t;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder = preorder;
        for(int i = 0; i < inorder.size(); i++) {
            index[inorder[i]] = i;
        }
        return settree(0, 0, preorder.size() - 1);
    }
};

BETTER SOLUTION

迭代

使用栈来储存当前遍历节点可能有右儿子的祖先节点（包括自己），使用index表示当前遍历节点的最左后代。preorder[0]为整颗树的根节点，初始化时将其入栈。inorder[0]为整棵树的最左节点，index初始化为0。从1开始遍历preorder，每个循环首先查看栈顶节点值是否和index节点值相等。若不相等，说明还未遍历到整棵树的最左节点，继续往左构建树，并将节点压栈。若相等，说明已经遍历到最左节点，将栈顶节点弹出，index+1，直到index节点值不等于栈顶节点值，或者直到栈为空。最后一个弹出的节点就是当前遍历节点的左父节点，连接后将其压栈。如此遍历完preorder，重建二叉树完成。

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (!preorder.size()) {
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[0]);
        stack<TreeNode*> stk;
        stk.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.size(); ++i) {
            int preorderVal = preorder[i];
            TreeNode* node = stk.top();
            if (node->val != inorder[inorderIndex]) {
                node->left = new TreeNode(preorderVal);
                stk.push(node->left);
            }
            else {
                while (!stk.empty() && stk.top()->val == inorder[inorderIndex]) {
                    node = stk.top();
                    stk.pop();
                    ++inorderIndex;
                }
                node->right = new TreeNode(preorderVal);
                stk.push(node->right);
            }
        }
        return root;
    }
};

SUMMARY

迭代法有点难以理解，需要结合代码多多复习。