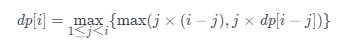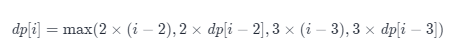Leetcode题解 剑指 Offer 14- II. 剪绳子 II

PROBLEM

剑指 Offer 14- II. 剪绳子 II

难度 中等

MY ANSWER

使用快速幂求余，使用long long防止溢出。尽量将绳子切成以3为单位，若余1则将一段变4，若余2则乘上2这段。数学原理可看这篇题解，主要使用均值不等式、导数来证明。时间复杂度O(1)，空间复杂度O(1)。

class Solution {
public:
    long long fpow(long long x, long long y) {
        long long res = x;
        long long ans = 1;
        while(y) {
            if(y & 1) {
                ans = ans * res  % 1000000007;
            }
            res = res * res  % 1000000007;
            y = y>>1;
        }
        return ans;
    }
    int cuttingRope(int n) {
        if(n == 2) {
            return 1;
        } 
        if(n == 3) {
            return 2;
        }
        if(n == 4) {
            return 4;
        }
        int res = n / 3;
        int rem = n % 3;
        if(rem == 0) {
            return fpow(3, res);
        }
        if(rem == 1) {
            long long tmp = fpow(3, res - 1) * 4 % 1000000007;
            return tmp;
        }
        if(rem == 2) {
            long long tmp = fpow(3, res) * 2 % 1000000007;
            return tmp;
        }
        return 0;
    }
};

BETTER SOLUTION

动态规划

创建数组 dp，其中 dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后，这些正整数的最大乘积。状态转移方程为

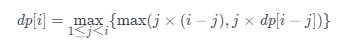
时间复杂度O(n^2)，空间复杂度O(n)。

class Solution {
public:
    int integerBreak(int n) {
        vector <int> dp(n + 1);
        for (int i = 2; i <= n; i++) {
            int curMax = 0;
            for (int j = 1; j < i; j++) {
                curMax = max(curMax, max(j * (i - j), j * dp[i - j]));
            }
            dp[i] = curMax;
        }
        return dp[n];
    }
};

状态方程还可根据和上面相似的数学原理优化为：

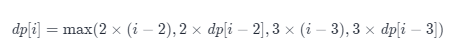
时间复杂度O(n)，空间复杂度O(n)。

class Solution {
public:
    int integerBreak(int n) {
        if (n < 4) {
            return n - 1;
        }
        vector <int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            dp[i] = max(max(2 * (i - 2), 2 * dp[i - 2]), max(3 * (i - 3), 3 * dp[i - 3]));
        }
        return dp[n];
    }
};

SUMMARY

记住该题面与数学结论，还有快速幂取余模板：

long long fpow(long long x, long long y) {
        long long tmp = x;
        long long res = 1;
        while(y) {
            if(y & 1) {
                res = res * tmp  % 1000000007;
            }
            tmp = tmp * tmp  % 1000000007;
            y = y>>1;
        }
        return res;
    }

以x^13为例	初值	1101	110	11	1
res	1	x	x	x^5	x^13
tmp	x	x^2	x^4	x^8	x^16

即x^13 = x ^ 1 * x ^ 4 * x ^ 8。